Wartość pieniądza w czasie

Jak podaje portal keepsimple.pl na wartość pieniądza w czasie wpływają dwie grupy czynników: związane z inflacją oraz z kosztem alternatywnym.

Pieniądz jutro będzie miał mniejszą wartość niż dzisiaj

We Wrocławiu, tuż przy ryneczku Psiego Pola, znajduje się budka z włoskimi lodami. Gdy byłem w szkole podstawowej, bardzo te lody lubiłem; pamiętam, że gdy miałem 12 lat, mały kosztował 1,20 zł. Załóżmy, że w czerwcu mogłem na ten cel przeznaczyć 25 zł, wystarczyłoby mi wówczas prawie na 21 lodów (20 groszy by zabrakło, ale stałemu bywalcowi raz można odpuścić). Co roku mały lód drożał o 10 groszy, w związku z czym moje 25 złotych wystarczało na coraz mniejszą ilość lodów. Po roku na 19, na osiemnastkę mógłbym kupić 13 lodów, a w wieku dwudziestu dwóch lat – 11.

Co się zmieniło między 2002, a 2012 rokiem? Waluta się nie zmieniła, w obiegu wciąż znajdowały się banknoty wydane pod koniec XX wieku. Ale nawet gdybym płacił w 2012 roku tymi samymi banknotami i monetami, co w 2002, zamiast 21 lodów dostałbym tylko 11. Jako jedenastolatek jeszcze o tym nie wiedziałem, ale dzisiaj wiem, że na własnej skórze doświadczyłem inflacji.

Wartość pieniądza w czasie można uznać za najważniejszą koncepcję finansową (Brigham i Houston: s. 162). Wpływają na nią dwie główne grupy czynników: związane z inflacją oraz z kosztem alternatywnym.

Inflacja

Inflacja to postępujący wzrost cen i związany z nim spadek siły nabywczej pieniądza. Innymi słowy, inflacja informuje o tym jak zmienia się jego siła nabywcza (Damodaran 2007: 509-513). Pieniądz jest nośnikiem wartości, a gdy jego wartość spada, za tę samą kwotę, kupić można mniej dóbr i usług.

Inflacja jest bardzo mocno powiązana z ilością pieniądza w gospodarce. W średniowieczu zjawisko to nazywano „psuciem monety”, a pisali o tym czeski kronikarz Kosmas (Wojciechowska 1968), wykładowca z Sorbony – Mikołaj z Oresme zwany też Orezmiuszem, Mikołaj Kopernik oraz Thomas Gresham (Morawski 2008: 48-49), wszyscy zgodnie twierdzili, że (za Kosmasem)

„żadna klęska, żadna zaraza ani śmiertelność (…) więcej by nie zaszkodziły ludowi Bożemu niż częsta zmiana i zdradliwe pogarszanie monety,”

czyli przetapianie monet na nowe, mniejsze i gorszej próby.

Wyraźne wzrosty inflacji na przestrzeni wieków związane były ze zwiększaniem podaży pieniądza (Phelps-Brown i Hopkins, 1956). Widać to na danych zbieranych od XIII wieku w Wielkiej Brytanii. Takie wydarzenia miały miejsce podczas podboju Szkocji i Walii w XIII wieku, wielkich zdobyczy kolonialnych na przełomie XVI i XVII wieku oraz podczas gorączki złota w Ameryce Północnej w XVIII wieku.

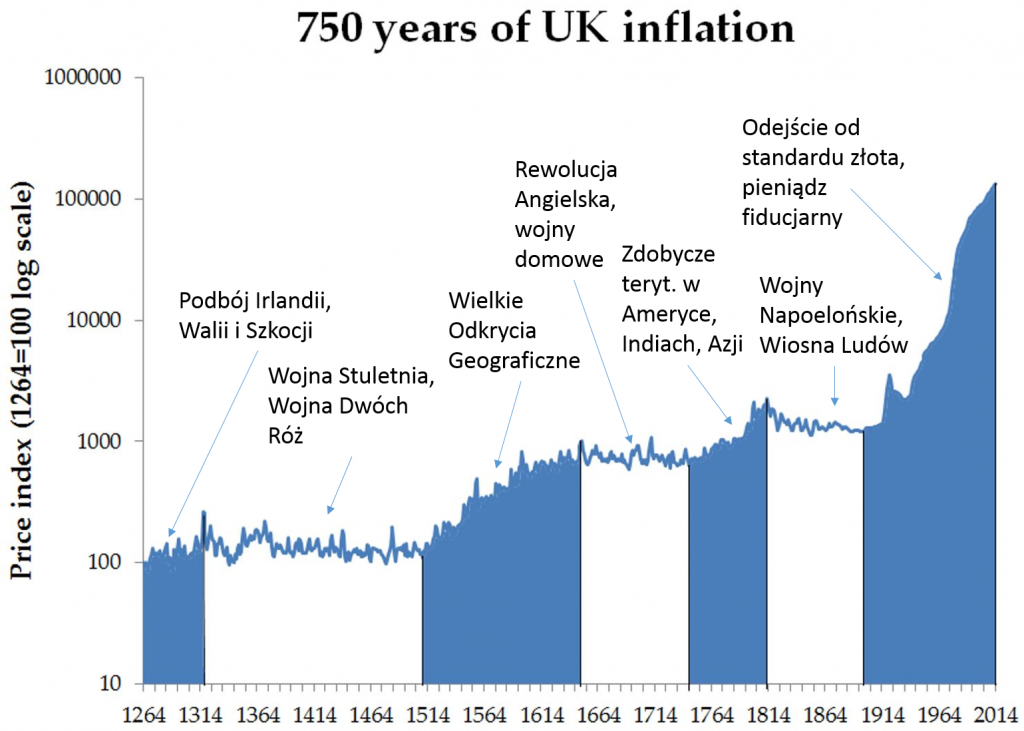
Wydarzenia rujnujące angielską (i brytyjską) gospodarkę – Wojna Stuletnia, Wojna Dwóch Róż, Rewolucja Angielska, Wojny Napoleońskie oraz Wiosna Ludów – powodowały deflację. Wartość pieniądza w tych czasach zachowywała się jeszcze w miarę naturalnie. Gdy gospodarka się rozwijała, pieniądza było więcej i ceny rosły, a w ciężkich czasach ilość pieniądza się zmniejszała, więc ceny spadały.

Punktem przełomowym, zmieniającym charakter inflacji, była Wielka Wojna. Jej uczestnicy zawiesili wymienialność pieniędzy na kruszec (standard złota), z obawy przed wykorzystaniem go przez wrogie państwa. Dość powszechne było jednak oczekiwanie, że po zakończeniu wojny wszystko wróci do normy.

Wojna finansowana była w dużej mierze polityką inflacyjną.

Po zakończeniu wojny, w latach dwudziestych, można było obserwować próby powrotu do stanu sprzed 1914. Okazało się to jednak nierealne, a jednym z efektów tych prób była deflacja, która w następnej dekadzie doprowadziła do wielkiego kryzysu gospodarczego w 1929 roku (Morawski 2008: 130-144). Po jego zakończeniu, w latach trzydziestych, państwa na całym świecie zaczęły odchodzić od standardu złota (Morawski 2008: 162-164).

Gdy pieniądz stał się fiducjarny, rządy mogły go emitować teoretycznie bez żadnych ograniczeń, a zjawisko inflacji stało się ważnym problemem dla rozwijających się nauk ekonomicznych.

Próba kontrolowania inflacji

Jak pamiętacie z rozdziału 7 wzrost gospodarczy wymaga utrzymywania stabilnych cen. Za to zadanie odpowiedzialni są emitenci pieniądza, czyli banki centralne i instytucje z nimi powiązane. W Polsce zadanie to spoczywa na Radzie Polityki Pieniężnej, która ustala stopy procentowe, po których Narodowy Bank Polski może pożyczać lub przyjmować na depozyt pieniądze od banków komercyjnych.

W mediach dosyć często można usłyszeć (lub przeczytać) o tym, że bank centralny podjął jakąś decyzję dotyczącą stóp procentowych (obniżył, podwyższył lub pozostawił na dotychczasowym poziomie). Są one jednym z kluczowych narzędzi, za pomocą których państwa starają się wpływać na inflację.

• Stopa referencyjna (opis NBP) (grudzień 2016: 1,50%) jest stopą po której przeprowadzane są operacje otwartego rynku.
• Stopa lombardowa (opis NBP) (grudzień 2016: 2,50%) określa cenę, po której bank centralny udziela bankom komercyjnym pożyczek pod zastaw papierów wartościowych.
• Stopa depozytowa (opis NBP) (grudzień 2016: 0,50%) określa oprocentowanie jednodniowych depozytów składanych przez banki komercyjne w banku centralnym.
• Stopa redyskontowa (opis NBP) (grudzień 2016: 1,75%) służy do obliczania ceny, po jakiej bank centralny przyjmuje do redyskonta spełniające określone warunki weksle od banków komercyjnych.

Warto się interesować decyzjami Rady Polityki Pieniężnej, ponieważ mają one istotny wpływ na całą krajową gospodarkę. Nie tylko na banki i przedsiębiorstwa, ale również na nas. Gdy stopy procentowe zostają podwyższone, rośnie koszt kredytów ale również stopy zwrotu z bezpiecznych inwestycji (lokat, obligacji). Gdy maleją, koszt kredytów (przynajmniej nominalny) spada, tak samo jak stopy zwrotu.

Od stopy lombardowej uzależnione jest maksymalne oprocentowanie, jakie pobrać mogą od nas banki.

Z kolei od stopy referencyjnej uzależnione są odsetki ustawowe. Ma ona również istotny wpływ na inną stopę procentową – WIBOR (Warsaw Interbank Offered Rate). Jest to stopa, po której banki komercyjne pożyczają sobie nawzajem pieniądze. Szczegóły jej ustalania można znaleźć na stronie stowarzyszenia ACI Polska, które zajmuje się ich ustalaniem (fixingiem).

Wróćmy jednak do tematu inflacji. Stopy procentowe na pewno mają na nią pewien wpływ, ale pamiętajcie (rozdział 7), że system gospodarczy jest bardzo skomplikowany.

Działa na nim wielu uczestników, którzy zawierają między sobą transakcje warte miliardy dolarów. Czasami może on przypominać przeciąganie liny – jedni ciągną w jedną stronę, a drudzy w przeciwną. Tyle, że tych lin jest bardzo, bardzo dużo, siły uczestników są bardzo nierówne, liny często pękają przewracając zawodników, którzy deptani są przez innych… dzieją się naprawdę ciekawe rzeczy.

Stopy procentowe to tylko jeden z wielu czynników, które wpływają na inflację. Jak wspomniałem na samym początku rozdziału, jest taki jeden czynnik, który ma duży wpływ na inflację. To podaż pieniądza.

Ukryty podatek

W obecnym systemie pieniądza fiducjarnego (opis NBP) inflacja jest stanem naturalnym. Rządy, nawet te kierujące się konserwatywną polityką pieniężną, w długim terminie drukują więcej pieniędzy, niż są warte towary i usługi produkowane w danym państwie. Wówczas łączna ilość pieniędzy wzrasta, podczas gdy PKB nie. Wartość nabywcza danej waluty spada – co odczuwają wszyscy – więcej pieniędzy ma jednak tylko rząd.

Janek, zaradny mieszkaniec Małomiasteczkowa, nauczył się idealnie podrabiać pieniądze. Jego banknoty są nie do odróżnienia od tych, drukowanych przez NBP. Jeżeli wydrukuje on 400.000 złotych i wprowadzi je do obiegu, odczują to wszyscy mieszkańcy Małomiasteczkowa. W gospodarce będzie więcej pieniędzy, jednak tyle samo towarów. Janek bardzo lubi pączki. Dlatego też gdy tylko nowe pieniądze były gotowe, poszedł do cukierni i kupił dwa opakowania, 12 sztuk. Cukiernik się zdziwił, ponieważ Janek zawsze kupował 2 pączki. W połowie dnia pączków zabrakło. Następnego dnia Janek znowu kupił 12 pączków, i ponownie ich zabrakło.
Cukiernik nie był w stanie upiec więcej pączków. Kiedyś gdzieś czytał o tym, czym jest rynek. Przypomniał sobie pojęcie ceny równowagi. Skoro nie może zwiększyć podaży, a popyt widocznie jest większy, powinien nieco zwiększyć ceny. I faktycznie, gdy następnego dnia cena pączków nieco wzrosła, ponownie zostały trzy pączki – akurat dla cukiernika.
Co się wydarzyło w Małomiasteczkowie? Janek sobie wydrukował pieniądze. Zaczął je wydawać w cukierni. Cukiernik widząc, że jego podaż nie zaspokaja nowego popytu, zwiększył cenę. Od tego momentu wszyscy płacą więcej, mimo że nie dostali żadnych dodatkowych pieniędzy. Ceny wzrosły, bo w gospodarce Małomiasteczkowa pojawiło się więcej pieniędzy. Wszyscy klienci cukierni, poza Jankiem, są poszkodowani.

Janek złamał prawo. Nie mógł sobie wydrukować pieniędzy, jest to bardzo surowo karalne przestępstwo. Jest jednak jedna organizacja, która może pieniądze sobie drukować. Dokładnie tak, jak zrobił to Janek. Tą organizacją jest Państwo. Dlatego właśnie inflacja jest ukrytym podatkiem. Państwo drukuje pieniądze, ma ich więcej, rynek odczuwa wzrost pieniądza, a w efekcie rosną ceny (Knott 2014).

Przechodząc z bajkowych historii do rzeczywistości, zobaczcie jak w Polsce wygląda podaż pieniądza. Na poniższym wykresie możecie zobaczyć, że w październiku 2016 Rzeczpospolita Polska wydrukowała dodatkowe 5,71 miliarda złotych. I nie był to jakiś szczególny miesiąc – wzrost ilości pieniądza w gospodarce jest mniej więcej stały.

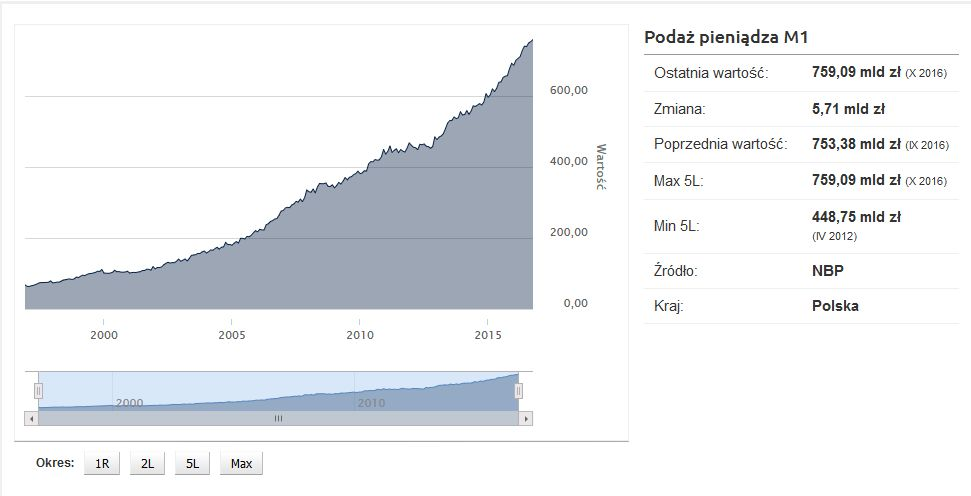
Państwa nie mogą drukować sobie pieniędzy tak o, bez ograniczeń. Cesarz Tyberiusz pouczał zarządców prowincji, że owce należy strzyc, a nie obdzierać ze skóry (Swetoniusz 121: III, 32) – zasada ta jest ponadczasowa. Podaż pieniądza musi więc być kontrolowana, ponieważ jeżeli zbyt dużo pieniędzy zostanie wydrukowanych, ich wartość nabywcza niebezpiecznie spadnie.

Niektórzy ludzie ograniczą wtedy swoje wysiłki (bo po co mam pracować ciężej, skoro nie żyje mi się lepiej?), dochody spadną – a wraz z nimi przychody z podatków. Będzie trzeba drukować więcej pieniędzy, inflacja jeszcze bardziej wzrośnie – w ten sposób nakręci się spirala inflacyjna.

Dlatego dodrukowane pieniądze do obrotu trafiają za pośrednictwem NBP. Bank centralny udziela pożyczek bankom komercyjnym, a te z kolei firmom i osobom fizycznym. Rząd nie może więc wykorzystać tych pieniędzy na łatanie dziury budżetowej lub własne potrzeby.

Drukowanie pieniędzy jest jednak potrzebne. Bank Centralny robi to po to, byśmy mieli czym płacić. Gospodarka nieustannie się rozwija (nowe technologie, lepsze produkty, tańsza produkcja, więcej zasobów naturalnych, itd.), pojawia się coraz więcej dóbr (towarów i usług). Gdyby ilość pieniądza się nie zmieniała, z czasem nie byłoby czym płacić. Wówczas pieniądz zaczął zyskiwać swoją własną wartość, więc zaczęlibyśmy płacić za to, że możemy z niego korzystać.

Firmy, produkując coraz więcej produktów, mogłyby gromadzić pieniądze. Z czasem mogłoby dojść do sytuacji, w której posiadanie pieniędzy byłoby symbolem prestiżu, a część społeczeństwa zostałaby wykluczona z systemu gospodarczego i musiała się wrócić w czasy barteru i produkcji domowej.

Wstrzymanie emisji pieniądza mogłoby się skończyć bardzo niebezpiecznym kryzysem całego systemu gospodarczego. By do tego nie dopuścić, banki centralne drukują pieniądze. Teoretycznie, powinny drukować ich tyle, by wartość pieniędzy była równa wytworzonej wartości (produkowanym towarom i usługom). W praktyce inflacja jest dla nas informacją, że emisja pieniądza jest większa niż wartość produkcji.

W historii ekonomii były różne „odpowiednie” poziomy inflacji. Obecnie uważa się, że powinna ona być niska, to znaczy na poziomie 2-3%. Ale nawet niska inflacja podlega działaniu procentu składanego (o którym w dalszej części rozdziału) – nie widać jej w krótkim okresie, ale im dłuższy okres, tym większe jej rozmiary.

Nawet niska inflacja w długim okresie jest istotna

By policzyć ile musi upłynąć czasu, by ceny się podwoiły, możemy zastosować Regułę 72:

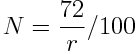
Załóżmy, że inflacja będzie wynosiła średnio 1,5%. Po ilu lat ceny się podwoją?

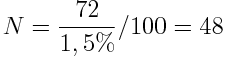
Oznacza to, że przy inflacji wynoszącej 1,5%, ceny podwoją się po 48 latach. Lody, które kupowaliście mając 12 lat, w wieku 60 lat byłyby dwukrotnie droższe. Kiedyś chleb kosztował 1 zł, dziś 2 zł. Kiedyś mieszkanie kosztowało 150.000, dziś 300.000. Ale pamiętajcie, że 1,5% to bardzo niska inflacja. Jakby wyglądały ceny, jeżeli NBP udałoby się utrzymać cel inflacyjny (2,5%)?

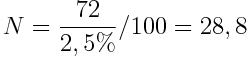
Ceny podwajałyby się prawie co 29 lat.

Magda, kupując sobie lody włoskie, w wieku dwunastu lat płaciła 1,20 zł, a jej mama 1200 zł za wynajem trzypokojowego mieszkania. W wieku 41 lat, dwunastoletnia córka Magdy za loda płaci 2,40 zł, a ona sama za wynajem trzypokojowego mieszkania 2400 zł. W następnym pokoleniu – wnuczka Magdy za loda zapłaci 4,80 zł, a córka za mieszkanie 4.800 zł.

Popatrzmy na to z innej strony.

Jacek nie ufa bankom, twierdzi, że to złodzieje. W Księdze Wyjścia jest napisane (Wj 22, 24):
Jeśli pożyczysz pieniądze ubogiemu z mojego ludu, żyjącemu obok ciebie, to nie będziesz postępował wobec niego jak lichwiarz i nie każesz mu płacić odsetek
A to co robią banki, to lichwa jak nic. Chciałby kupić swojemu dziecku mieszkanie, na prezent z okazji ukończenia studiów – czyli za 28 lat (o dziecko wraz z żoną zamierzają się starać za 3 lata). Mieszkanie kosztuje 300.000 złotych. Jacek policzył, że musi odkładać 892,86 złotych miesięcznie. I odkłada tę kwotę do skarbonki przez 28 lat. Oglądał Zeitgeist: Pieniądz rządzi światem i nie odda bankom swoich pieniędzy.
Syn kończy studia. Był wspaniałym dzieckiem – prezent mu się należy. Okazuje się jednak, że mimo, odłożonych 300.000 złotych, nie starczy na mieszkanie. Brakuje… 300.000 złotych. Mieszkanie kosztuje teraz 600.000 złotych, jego cena wzrosła pod wpływem samej inflacji, sytuacja na rynku nieruchomości się nie zmieniła. A przecież wszyscy zawsze powtarzali, że inflacją się nie trzeba przejmować, bo jest na niskim poziomie…

Jak więc widzicie, w szacunkach długoterminowych nie można pominąć inflacji. Trzeba ją w jakiś sposób uwzględnić.

Koszt alternatywny

Wrócimy do tego tematu, teraz jednak zostawmy inflację, a zwróćmy uwagę na drugi czynnik wpływający na wartość pieniądza w czasie, czyli koszt alternatywny.

Za każdym razem, gdy wydajemy na coś pieniądze, pozbawiamy się możliwości ich zainwestowania. W podręcznikach i opracowaniach naukowych jako przykład podaje się możliwość inwestycji wolnej od ryzyka, czyli bony skarbowe i obligacje skarbu państwa.

Darek uważa, że bezpiecznymi instrumentami są obligacje korporacyjne większych przedsiębiorstw (notowanych na WIG 30), natomiast obligacje czy bony skarbowe, a nawet lokaty bankowe – to są instrumenty higieniczne. Chce kupić dla Magdy telewizor za 2.000 złotych. Tuż przed wyjściem do sklepu zobaczył na mailu informację o emisji obligacji przez Kruk S.A. – oprocentowanie na poziomie 3% ponad WIBOR 3M w skali roku. Gdyby miał wybór (wszyscy dobrze wiemy, że tak naprawdę go nie ma), to jego koszt alternatywny zakupu telewizora wyniósłby:
2000 + zysk z obligacji – podatek „Belki”
Telewizor używany będzie przez trzy lata, tyle samo wynosi termin zapadalności (po rozdziale 11 wiecie co to znaczy) obligacji. Pomińmy fakt, że odsetki są kapitalizowane co kwartał – dla uproszczenia założymy najprostszą sytuację, czyli kapitalizacja odsetek raz w roku.
Używając wzoru na przyszłą wartość (FV) obliczyłem, że Darek otrzymałby po trzech latach 2302,05 zł (dla uproszczenia założyłem, że WIBOR 3M będzie na poziomie 1,8% przez cały okres inwestycji). Darek będzie musiał jeszcze zapłacić podatek od zysków kapitałowych (302,05 * 19%) w wysokości 57,39 zł, czyli ostatecznie z inwestycji w obligacje firmy Kruk S.A. otrzymałby 2244,66 zł. To jest jego koszt alternatywny, ponieważ gdyby Magda nie kazała mu kupić telewizora, zainwestowałby. Tyle też za 3 lata będzie warte jego dzisiejsze 2.000 zł.

Jeszcze wyraźniejszy przykład (książkowy) jest następujący:

Możesz otrzymać 2000 zł dzisiaj lub 2200 złotych za trzy lata. Stopa zwrotu wynosi 4,8%. Co wybierasz?
Obliczyliśmy już wcześniej, że Darkowi bardziej będzie się opłacało otrzymać 2000 dzisiaj, ponieważ przy zainwestowaniu tych środków otrzyma 2244,66 zł. Ale Jacek nie odważyłby się zainwestować w obligacje korporacyjne Kruka. Przecież to firma – może upaść! Po rozmowie z Darkiem (przyjaźnią się) zgodził się jednak spróbować zainwestować 2000 złotych. Znalazł lokatę oprocentowaną na poziomie 2,5%. Co dla niego byłoby lepsze – zainwestować te 2000 złotych w lokatę, czy otrzymać za trzy lata 2200 zł?

Wartość przyszła, wartość bieżąca

Wzór na Wartość Przyszłą (FV):
FV = PV * (1 + r)n
FV = 2000 * (1+0,025)3 = 2153,78
Jacek powinien więc zgodzić się na drugą opcję – za trzy lata dostać 2200 zł.

Gdy odwrócimy ten wzór, będziemy mogli zdyskontować, czyli obliczyć obecną wartość (PV).

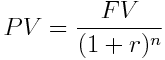
Dyskontowanie przyda nam się podczas uwzględniania inflacji.

Darek chce wziąć kredyt na samochód za 45.000 złotych. Jego doradca finansowy przesłał mu kilka najlepszych ofert, z których wyróżniają się trzy:

Bank	Kwota	Oprocentowanie	Prowizja
A	36.000 zł	6%	0%
B	45.000 zł	5%	5%
C	45.000 zł	8%	0%

Darek chce jak najtańszy kredyt, to znaczy, że chce rzeczywiście zapłacić jak najmniej. Wie, co to inflacja i chce ją uwzględnić. W dniu udzielenia kredytu wynosiła 2,5%; jako że jest to cel inflacyjny NBP, Darek przyjął, że pozostanie na tym poziomie przez cały okres kredytowania.

Darek policzył obecną wartość (PV) wszystkich przepływów pieniężnych.

Pierwszy przepływ pieniężny w przypadku oferty A wynosi 9.000 złotych o wartości 100%, ponieważ za wartość realną będziemy uznawać wartość nominalną z dnia wypłaty kredytu. Przepływy w kolejnych okresach podałem w tabeli:

Bank	1 przepływ	Kolejne przepływy	Suma nominalna
A	9000	455,76	52.752,96
B	2250	569,70	56.941,20
C	0	636,15	61.070,40

Według symulacji doradcy finansowego, najlepsza wydaje się być oferta A, natomiast ofertę C radził odrzucić. Według niego bank B mógłby być bankiem awaryjnym, gdyby coś poszło nie tak w A. Darek przeczytał na stronie KeepSimple.pl jak obliczyć rzeczywisty koszt kredytu i postanowił sprawdzić, czy doradca finansowy miał rację. Rzeczywiste koszty kredytów wyniosły odpowiednio:

Bank A	Bank B	Bank C
48 618,06 zł	51 772,58 zł	55 298,91 zł

Tak więc doradca finansowy miał rację, najkorzystniejsza była oferta A, a najmniej korzystna oferta C. Jednakże różnice między nimi były mniejsze niż wydawało się to nominalnie. Nominalnie bank B był tańszy od C o 4129,20 zł, a rzeczywiście 3526,33 zł; z kolei bank A był tańszy od B nominalnie o 4188,24 zł, a realnie 3154,22 zł, a od C o 8317,44 zł nominalnie (6680,85 zł realnie).

Darek sprawdził też, jak zachowywać się będą oferty pod wpływem zmiany inflacji. Ofertę A można uznać za bezpieczną. Inflacja musiałaby wynieść średniorocznie13,5%, by stała się ona mniej opłacalna niż oferta B. Obniżenia inflacji testować nie trzeba, ponieważ taka sytuacja powiększałaby tylko różnicę między ofertami na korzyść A.

Procent składany

W rozdziale pojawiło się już pojęcie procentu składanego. Jest to dosyć popularne określenie, padające często (niestety) z ust sprzedawców funduszy inwestycyjnych i produktów opartych o fundusze. Procent składany to sposób oprocentowania polegający na tym, że odsetki za dany okres również są kapitalizowane. To znaczy, że nie są wypłacane, tylko dodawane do kwoty inwestycji – tak jak w przypadku inwestycji Darka w obligacje Kruka oraz Jacka w lokatę.

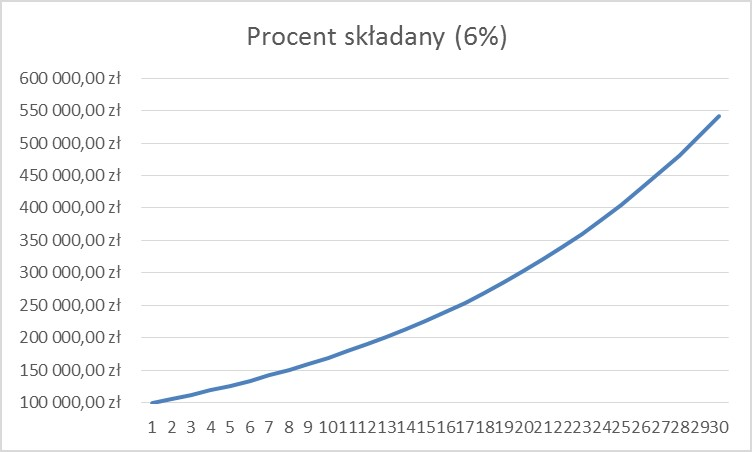
Inwestując w fundusze pamiętajcie jednak, że procentu składanego tam nie ma. Jest to bowiem inwestycja jednorazowa, fundusze nie wypłacają nam odsetek, a więc nie są one reinwestowane. Dla zwrotu z funduszu nie liczymy procentu składanego, tylko oprocentowanie średnioroczne.

Inflacja stanowi natomiast przeciwieństwo procentu składanego, czyli dyskonto składane – kolejne dyskonta są naliczane od coraz niższych kwot. Łatwiej to zrozumieć patrząc na poniższe wykresy.

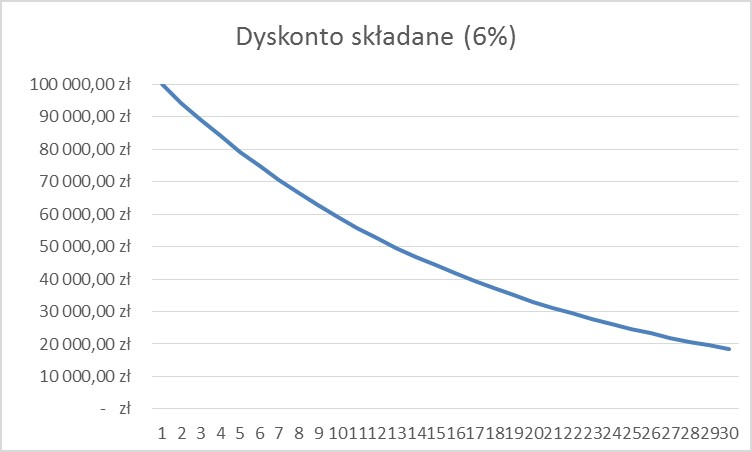
Ostatnią na dzisiaj kwestią jest rzeczywista stopa procentowa, czyli sposób liczenia opłacalności inwestycji z uwzględnieniem inflacji. Zobaczmy, jakie rzeczywiste oprocentowanie uzyskali Darek oraz Jacek.

Wzór na rzeczywistą stopę procentową:

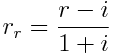
gdzie:

r_r – rzeczywista stopa procentowa

r – nominalna stopa procentowa

i – stopa inflacji

Załóżmy, że inflacja (średniorocznie) wyniesie 1%.

Inwestycja Darka

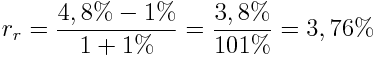
Inwestycja Jacka

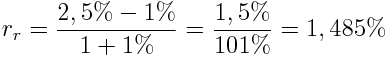
Rozumiem, że powyższe wzory mogą was przerażać. Niepotrzebnie. Nie musicie tego liczyć – wystarczy, że będziecie sobie zdawać sprawę z tego, czym jest wartość bieżąca (PV), wartość przyszła (FV) oraz kiedy się je liczy, a także jaka jest różnica między stopą nominalną, a stopą rzeczywistą.

Wartość przyszłą oraz wartość bieżącą policzycie tutaj:

http://www.calculator.net/finance-calculator.html

(Wartość przyszła w zakładce „FV”, a wartość bieżąca w zakładce „Start Principal”).

Rzeczywistą stopę procentową policzycie tutaj:

http://www.mathcelebrity.com/inflation.php?nir=4.8&i=1&rri=&pl=Calculate

(wprowadziłem dane dla inwestycji Darka).

Streszczenie:

Wartość pieniądza w czasie można uznać za najważniejszą koncepcję finansową. Wpływają na nią dwie grupy czynników: związane z inflacją oraz z kosztem alternatywnym. Inflacja to postępujący wzrost cen i związany z nim spadek siły nabywczej pieniądza. Innymi słowy, inflacja informuje o tym jak zmienia się jego siła nabywcza. Jest ona mocno powiązana z ilością pieniądza w gospodarce.

Gdy w trakcie Wielkiej Wojny zrezygnowano ze standardu złota na rzecz pieniądza fiducjarnego, podaż pieniędzy stała się teoretycznie nieograniczona. Zapoczątkowało to etap nieustannej inflacji, wskutek ciągłego dodrukowywania pieniędzy przez rządy państw. Negatywne doświadczenia z wysoką inflacją zmobilizowały jednak państwa, do utrzymywania niskiej inflacji. Głównym narzędziem służącym do kontrolowania inflacji są stopy procentowe, które w Polsce ustala Rada Polityki Pieniężnej. Mają one istotny wpływ na gospodarkę, ponieważ zależy od nich koszt pieniądza (kredytów i pożyczek) oraz zwrot z inwestycji.

Nawet niska inflacja w odpowiednio długim horyzoncie czasu potrafi w pewnym okresie podwoić ceny. Prostym sposobem na obliczenie tego okresu jest Reguła 72. Wpływ inflacji na inwestycje sprawdza się natomiast licząc rzeczywistą stopę procentową.

Za każdym razem, gdy wydajemy na coś pieniądze, pozbawiamy się możliwości ich zainwestowania. Wysokość odsetek jakie możnaby otrzymać z takiej inwestycji określa koszt alternatywny naszych decyzji, wyznaczając jednocześnie wartość pieniądza w czasie. Przyszłą wartość pieniądza oblicza się według wzoru na FV, natomiast obecną wartość pieniądza ze wzoru na PV. Obliczenie PV polega na dyskontowaniu FV. Obliczenie przyszłej wartości pieniądza wykorzystuje mechanizm procentu składanego.

Źródło: http://keepsimple.pl/elementarz/wartosc-pieniadza-czasie/